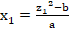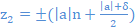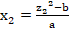| ax2 + bx + c = z2 |
Théorème 1a
Soient a et b deux entiers relatifs non nuls, ax + b est carré parfait si et seulement s’il existe au moins un entier  où k ∈ N = {0, 1, 2, 3, …} où k ∈ N = {0, 1, 2, 3, …}
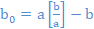 , ([b/a] représente la partie entière de b/a) , ([b/a] représente la partie entière de b/a)
Pour chaque entier δ, les solutions entières de cette équation sont :
|
- Soient a et b deux entiers relatifs non nuls, pour résoudre l’équation ax + b = carré parfait (où x doit aussi être un entier) :
- on calcule d’abord l’entier
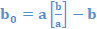 où [b/a] représente la partie entière de b/a.
où [b/a] représente la partie entière de b/a. - ensuite on calcule l’ensemble des valeurs positives, si elles existent, de
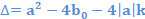 en commençant par k=0, k=1, k=2… ainsi de suite jusqu’à ce que la valeur de Δ soit négative.
en commençant par k=0, k=1, k=2… ainsi de suite jusqu’à ce que la valeur de Δ soit négative.
- Si aucune valeur de √∆ n’est un nombre entier, alors ax + b n’est pas un carré parfait.
- Si au moins une valeur de √∆ est un nombre entier, alors ax + b = z2 admet un nombre infini de solutions.
- on calcule d’abord l’entier
- b0 < |a|
- δ ≤ |a|, (si δ = a, alors z1 = z2 = |a|n)
- Si ax + b est carré parfait, alors le nombre de solutions est infini
- Pour chaque entier δ, les solutions z forment des suites arithmétiques de raison |a| et de premiers termes (|a| – δ)/2 pour z1 et (|a| + δ)/2 pour z2
- Calculer l’ensemble des entiers x pour que 17x – 11 soit carré parfait.
b0 = 17[(-11) / 17] – 11 = 17 x 0 – 11 = -11 Δ = 172 + 44 – 68k = 333 – 68k (k∈N)
Aucune valeur de δ n’appartient à N, donc il n’existe pas d’entier x tel que 17x – 11 = carré parfait.k = 0 1 2 3 4 Δ = 333 265 197 129 61 δ = √∆ = ∉ N - 7x + 28 peut-il être carré parfait ?
b0 = 7[28 / 7] – 28 = 0 Δ = 72 – 0 – 28k = 49 – 28k, (k∈ℵ)
δ = a donc z1 = z2 = an. z = 7n,k = 0 1 Δ = 49 21 δ = √∆ = 7 ∉ N 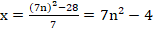
7x + 28 est carré parfait si x est de la forme 7n2 – 4, (n∈N)
L’ensemble des solutions est S = {-4; 3; 24; 59; 108; 171; 248; 339; 444; …}δ = 7 n = 0 1 2 … z = 0 7 14 x = -4 3 24 - Calculer l’ensemble des solutions de -8x + 33 = z2.
b0 = -8[33 / (-8)] – 33 = -1 Δ = (-8)2 + 4 – 32k = 68 – 32k, (k∈N)
δ = {2; 6}k = 0 1 2 Δ = 68 36 4 δ = √∆ = ∉ N 6 2
L’ensemble des solution est S = {… -62; -51; -41; -32; -24; -17; -11; -6; -2; 1; 3; 4}δ = 6 n = 0 1 2 … z1 = 1 9 17 x1 = 4 -6 -32 z2 = 7 15 23 x2 = -2 -24 -62 δ = 2 n = 0 1 2 … z1 = 3 11 19 x1 = 3 -11 -41 z2 = 5 13 21 x2 = 1 -17 -51
Le contenu de ce site est un texte original
Merci de faire référence à ce site ou son auteur lorsque vous citez ses formules
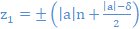 , (n∈N)
, (n∈N)